直交表を利用した組み合わせテスト
8月16日、炎天下の中でバーベキューをしたら日焼けというか火傷で顔と腕が痛いwata19です。
品質管理の業務にて膨大な数のパターン網羅をすることになり、現在、「直交表を利用した組み合わせテスト」を勉強中です。今回は直交表とは何かを解説します。(統計学や数学の観点は一切排除、分かり易さを心掛け、入門編として書いてみました。)
直交表では、まず因子と水準を決定します。因子とはテスト対象となるパラメータ、要素のことです。水準とは因子に許可される値の数のことで、例えば性別であれば男性、女性の2種類の値なので2水準となります。
直交表とは、任意の2因子(列)にて、とり得る選択肢(水準)の全ての組合せが同数回ずつ現れるという性質を持ったテストの為の割り付け表です。テストケースは最低でも因子の水準数の積のパターン数が必要となり、因子数が多くなるとパターン数は膨大な数になってしまいます。ところが、直交表を用いることによって、多くの因子に関するテストパターンを比較的少ない数にすることができます。
まずは、直交表を用いないときのテストケース。例えばOS(Windows XP、Windows Vistaの2通り)、ブラウザ(IE、Firefoxの2通り)、解像度(800×600、1024×768の2通り)といった組み合わせのテストケースを作成します。
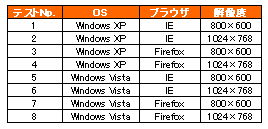
直交表を用いない場合、上記の画像のように8つのテストケースが必要となります。
今回は最も小さな直交表である「直交表L4」を用いて解説します。(直交表の名称であるLxxの「XX」部分は直交表の大きさを表しています。L4だと、4つのテストケースができることを意味します。)
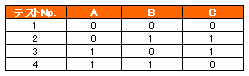
上記の画像にて、A、B、Cは3つの因子を表し、表中の各セルの0、1はそれぞれの因子における水準を表しています。つまり、因子Aには0と1という水準があるということです。
因子と水準がOS(Windows XP、Windows Vistaの2通り)、ブラウザ(IE、Firefoxの2通り)、解像度(800×600、1024×768の2通り)といった場合、表中のAを「OS」に書き換え、A列中の「0」を「Windows XP」、「1」を「Windows Vista」にそれぞれ書き換えます。このことを「直交表に割り付ける」といいます。
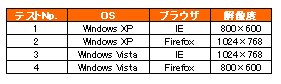
上記画像は割り付けを終えたものです。この4回のテストの中には、OSとブラウザの全組み合わせ(4通り)、ブラウザと解像度の全組み合わせ(4通り)、解像度とOSの全組み合わせ(4通り)が組み込まれています。
直交表はどれか2つの因子同士の組み合わせだけをテストするのではなく、同時に他の因子の組み合わせについてもテストをしています。このため、全パターン網羅よりもテストケースが少なくて済むということになります。
全ての組み合わせをテストしようとすると、因子と水準の値が増えるにしたがって無限大にテストケースが増えていくことになります。限られた期間の中でこれを達成するのはとても困難なことです。そこで、直交表を利用することで、全体の組み合わせの中から特に重要なサブセットを抜き出してテストしよう、ということです。
但し要注意なのは、直交表はあくまでサブセットであり、全組み合わせを網羅するものではないということです。例でいえば、全8通り – 直交表の4通り = 直交表で省かれた残りの4通りの組み合わせは考慮されないということです。考慮されなかった組み合わせでバグが検出されるリスクはあります。しかし、任意の2列間での全組み合わせは4通りでカバーできる。これが直交表の強みです。
次回は「直交表の多水準直交表への変形」について解説する予定です。
参考文献:
日科技連出版社
ソフトウェアテストHAYST法入門 品質と生産性がアップする直交表の使い方


ディスカッション
コメント一覧
まだ、コメントがありません